Quand les mathématiques permettent de modéliser la transition de l'économie.
Par Charles AIVAR
Comment modéliser la transition économique ? Comment relier "croissance débridée", "décroissance" et "post-croissance" ? Et qu'est-ce que cela dit de notre façon de "refermer/sacrifier" le futur ou de "l'ouvrir/le repossibiliser".
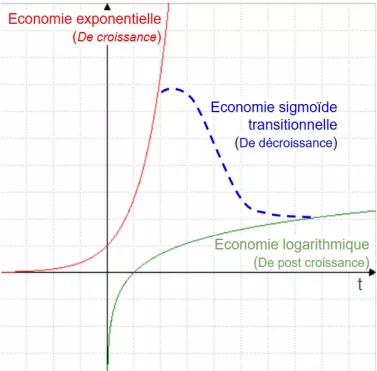
Nous sommes dans une économie de la croissance à accélération accélérée. Croissance tenue à bout de bras, jusqu'à l'aveuglement, pour ne pas avoir à réformer le modèle. Ce mécanisme est modélisé par la fonction exponentielle (exp(x) - courbe rouge). Plus le temps avance, plus la courbe monte vite. Chaque pas de temps impose une croissance dont le coût environnemental pèse de plus en plus lourd. Et pour maintenir cette croissance vertigineuse, on tape dans les stocks. On obère le futur. On brise les équilibres. On détruit les écosystèmes. On rend le futur inhabitable. On l'empêche d'advenir au profit d'une économie zombie, qui ne produit rien qu'un volume déshumanisé, déshumanisant, morbide et mortifère.
Le sens ? Aucun ! Sinon fournir aux "morts" qui nous gouvernent l'illusion d'une vie.
Tous les mathématiciens et j'imagine les économistes (quoique j'en doute de plus en plus) connaissent les propriétés TERRIFIANTES de la fonction exponentielle non pas en tant qu'elle est ce qu'elle est. C'est un objet mathématique extrahordinaire, mais qui ne doit pas être appliquée à une réalité matérielle ou alors sur un segment temporel fini, donc maitrisable. Pourquoi ? Parceque cette fonction est sa propre dérivée, ce qui signifie que l'accélération de sa verticalisation est elle même accélérée, et ainsi de suite...sans fin. Pour le dire autrement, plus ça va vite et plus ça accelère pour aller encore plus vite. Le prix de cette accélération ? Une exploitation débridée de TOUT, l'eau, les matières premières, les energies, les personnes, et par là même, cette folie anthropique démultiplie à la même vitesse ses conséquences entropiques: pollutions, destructions, destabilisation et enfante le capitalisme imperialiste de la finitude que nous voyons naitre sous nos yeux.
La fonction exponentielle est terrifiante parce qu’elle crée un emballement dans lequel continuer est destructeur, s’arrêter est catastrophique, ralentir est impossible. L'exponentielle n'est pas une opinion politique, c’est un piège logique, dans lequel les économistes sont tombés, séduits par sa facilité d'exploitation et son comportement favorable "avant le coude" sur ]-inf;0].
L'exponentielle n'a aucun frein interne. Elle est mathématiquement aveugle à la finitude.
Imaginons maintenant une économie de l'après, de la post croissance. (Pas de la non-croissance !) Une économie à la croissance infiniment ralentie qui s'inscrit dans la lenteur et dans le temps. Une économie naturaliste, ajustée aux rythmes du vivant, mue par la sagesse de faire aujourd'hui pour que cela advienne demain. Une économie du jardinier. Cela se traduit en mathématiques par la fonction logarithme (ln(x) - courbe verte). Cette fonction modélise une économie du ralentissement, de la limite, de la suffisance, de la patience, de la lenteur, de la frustration, et donc du sens et de la transcendance. Une économie qui justifie la difficulté du présent dans la satisfaction de voir un futur advenir. C'est une économie de la naissance, de la lignée, de la (re)génération. Si il y a un temps à "sacrifier" c'est le présent, expliqué par des gouvernants porteurs de sens, d'horizon, de vision.
La dérivée de la fonction Ln(x) est 1/x, ce qui traduit un ralentissement de son comportement. Plus on avance dans le temps, plus la courbe croit lentement, et si on dérive une seconde fois, on obtient -1/x², ce qui signifie que l'acceleration de sa croissance est négative, dont là encore on a un facteur de ralentissement supplémentaire. Ln(x) est la fonction inverse d'exponentielle, elle est son frein mathématique (et naturel). Et n'allez pas croire qu'elle finit par arrêter sa croissance. Non ! elle n'a pas d'assymptote, donc pas de plafond, mais une croissance infiniement ralentie. En tout cas en mathématique. Dans le monde réel il est fort à parier qu'elle arrivera à un point de stabilisation, totalement compatible avec le plafond de la théorie du Donut de Claire Raworth.
Comment on organise la transition puisque les courbes exponentielle et logarithme, ne se croisent pas. Elles n'ont pas d'existence commune, de point d'intersection. Donc, pour passer de l'une à l'autre, de l'économie de croissance à l'économie de post croissance, il faut une passerelle. Une troisième fonction mathématique : la sigmoïde, que nous appellerons la "fonction d'effondrement", et qui matérialise une économie transitoire de décroissance. Une économie de bifurcation, sorte de parachute institutionnel qui vise l'instauration d'un nouveau paradigme économique logarithmique. Une économie de réouverture portée par des dirigeants conscients et décidés à réinsuffler le sens, à renouer avec notre nature profonde, et à recoder l'économie pour en faire un outil au service d'une humanité (re)inscrite dans un futur.
exp(x) s’effondre necessairement dans la réalité par négation du réel. Sa direction assymptotique verticale n'est pas compatible avec un monde aux ressources limitées.
Ln(x) émerge des ruines, par continuité avec la sigmoide, et se redresse poussée par une autre logique de croissance. La logique de l'acceptation des limites, de la nécessaire regéneration du vivant et du reinvestissement du futur.
Croissance, décroissance, post-croissance ne sont pas des concepts à opposer. Il n'y a pas de choix à faire. Il faut juste les articuler dans le temps pour nous offrir la possibilité d'un avenir réouvert.
Il est grand temps que l'économie fasse sa révolution copernicienne. Elle est un des derniers bastions de l'obscurentisme scientifique. Mais l'économie est-elle une science ?
Dernière mise à jour : 25/01/2026